I am a CNRS researcher in statistical signal processing and machine learning, currently with the GAIA (Geometrie Apprentissage Information et Algorithmes) team in the GIPSA laboratory, in Grenoble, French Alps.
Research keywords: graph signal processing, spectral clustering, sampling methods, determinantal point processes, random processes on graphs
Internship positions
Internship positions are available on graph signal processing, determinantal point processes, community detection, machine learning. Please inquire by sending an e-mail at firstname.lastname [at] gipsa-lab.grenoble-inp.fr !
Current research interests
Graph Tikhonov regularization and interpolation via random spanning forests
denoising or interpolating a graph signal via random spanning forests
Novel Monte Carlo estimators are proposed to solve
both the Tikhonov regularization (TR) and the interpolation
problems on graphs. These estimators are based on random
spanning forests (RSF), the theoretical properties of which enable
to analyze the estimators’ theoretical mean and variance. We also
show how to perform hyperparameter tuning for these RSFbased estimators. TR is a component in many well-known algorithms, and we show how the proposed estimators can be easily
adapted to avoid expensive intermediate steps in generalized
semi-supervised learning, label propagation, Newton’s method
and iteratively reweighted least squares. In the experiments, we
illustrate the proposed methods on several problems and provide
observations on their run time. Details may be found here and the code here.
DPPs in the flat limit
what happens to an L-ensemble when the kernel function tends to the flat limit?
Determinantal point processes (DPPs) are repulsive point processes
where the interaction between points depends on the determinant of a
positive-semi definite matrix.
In this paper, we study the limiting process of L-ensembles based on kernel matrices, when the kernel function becomes flat (so that every point interacts with every other point, in a sense). We show that these limiting processes
are best described in the formalism of extended L-ensembles and partial projection DPPs, and the exact limit depends mostly on the smoothness of the
kernel function. In some cases, the limiting process is even universal, meaning that it does not depend on specifics of the kernel function, but only on its
degree of smoothness.
Since flat-limit DPPs are still repulsive processes, this implies that practically useful families of DPPs exist that do not require a spatial length-scale
parameter. Details may be found here.
Spectral Clustering in Sparse Graphs
unifying methods from statistical physics, machine learning and statistics for the hard problem of spectral clustering in sparse graphs
This article considers spectral community detection in the regime of sparse networks with
heterogeneous degree distributions, for which we devise an algorithm to efficiently retrieve
communities. Specifically, we demonstrate that a well parametrized form of regularized
Laplacian matrices can be used to perform spectral clustering in sparse networks without
suffering from its degree heterogeneity. Besides, we exhibit important connections between
this proposed matrix and the now popular non-backtracking matrix, the Bethe-Hessian
matrix, as well as the standard Laplacian matrix. Interestingly, as opposed to competitive
methods, our proposed improved parametrization inherently accounts for the hardness of
the classification problem. These findings are summarized under the form of an algorithm
capable of both estimating the number of communities and achieving high-quality community
reconstruction. Details may be found here and the code here.
Extended L-ensembles
bridging the gap between L-ensembles and DPPs
Determinantal point processes (DPPs) are a class of repulsive point processes, popular for their relative simplicity. They are traditionally defined via
their marginal distributions, but a subset of DPPs called "L-ensembles" have
tractable likelihoods and are thus particularly easy to work with. Indeed, in
many applications, DPPs are more naturally defined based on the L-ensemble
formulation rather than through the marginal kernel.
The fact that not all DPPs are L-ensembles is unfortunate, but there is a
unifying description. We introduce here extended L-ensembles, and show that
all DPPs are extended L-ensembles (and vice-versa). Extended L-ensembles
have very simple likelihood functions, contain L-ensembles and projection
DPPs as special cases. From a theoretical standpoint, they fix some pathologies in the usual formalism of DPPs, for instance the fact that projection DPPs
are not L-ensembles. From a practical standpoint, they extend the set of kernel
functions that may be used to define DPPs: we show that conditional positive
definite kernels are good candidates for defining DPPs, including DPPs that
need no spatial scale parameter.
Finally, extended L-ensembles are based on so-called "saddle-point matrices", and we prove an extension of the Cauchy-Binet theorem for such
matrices that may be of independent interest. Details may be found here.
Past research interests
Determinantal Point Processes for Coresets
efficiently creating summaries of large datasets that both preserve diversity and guarantee a low relative error for a given learning task
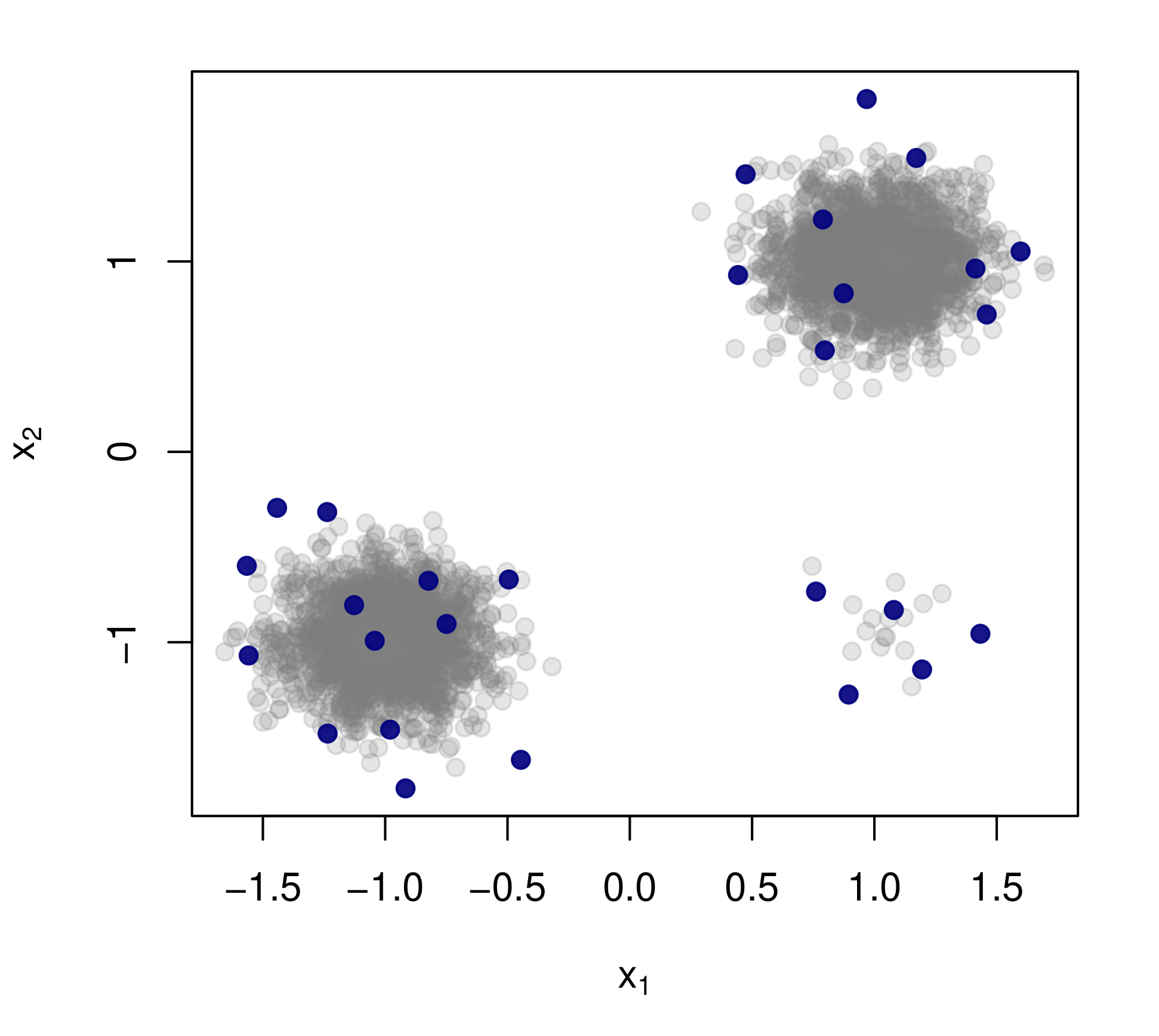When faced with a data set too large to be processed all at once, an obvious solution is to retain only part of it. In practice this takes a wide variety of different forms, and among them “coresets” are especially appealing. A coreset is a (small) weighted sample of the original data that comes with the following guarantee: a cost function can be evaluated on the smaller set instead of the larger one, with low relative error. For some classes of problems, and via a careful choice of sampling distribution (based on the so-called “sensitivity” metric), iid random sampling has turned to be one of the most successful methods for building coresets efficiently. However, independent samples are sometimes overly redundant, and one could hope that enforcing diversity would lead to better performance. The difficulty lies in proving coreset properties in non-iid samples. We show that the coreset property holds for samples formed with determinantal point processes (DPP). DPPs are interesting because they are a rare example of repulsive point processes with tractable theoretical properties, enabling us to prove general coreset theorems. We apply our results to both
the k-means and the linear regression problems, and give extensive empirical evidence that the small additional computational cost of DPP sampling comes with superior performance over its iid counterpart. Of independent interest, we also provide analytical formulas for the sensitivity in the linear regression and 1-means cases. Details may be found here and the code here.
Revisiting the Bethe-Hessian: Improved Community Detection in Sparse Heterogeneous Graphs
spectral clustering with the Bethe-Hessian: an improved parametrization to take into account heterogeneous degree distributions in sparse graphs
Spectral clustering is one of the most popular, yet still incompletely understood, methods for community detection on graphs. This article studies spectral clustering based on the Bethe-Hessian matrix $H_r = (r^2 − 1)In + D − rA$ for sparse heterogeneous graphs (following the degree-corrected stochastic block model) in a two-class setting. For a specific value $r = \zeta$, clustering is shown to be insensitive to the degree heterogeneity. We then study the behavior of the informative eigenvector of $H_\zeta$ and, as a result, predict the clustering accuracy. The article concludes with an overview of the generalization to more than two classes along with extensive simulations on synthetic and real networks corroborating our findings. Details may be found here and the code here.
Asymptotic Equivalence of Fixed-size and Varying-size Determinantal Point Processes
efficient and numerically stable approximate sampling of fixed-size DPP (so-called k-DPPs)
Determinantal Point Processes (DPPs) are popular models for point processes with repulsion. They appear in numerous contexts, from physics to graph theory, and display appealing theoretical properties. On the more practical side of things, since DPPs tend to select sets of points that are some distance apart (repulsion), they have been advocated as a way of producing random subsets with high diversity. DPPs come in two variants: fixed-size and varying-size. A
sample from a varying-size DPP is a subset of random cardinality, while in fixed-size “k-DPPs” the cardinality is fixed. The latter makes more sense in many applications, but unfortunately their computational properties are less attractive, since, among other things, inclusion probabilities are harder to compute. In this work we show that as the size of the ground set grows, k-DPPs and DPPs become equivalent, in the sense that fixed-order inclusion probabilities converge. As a by-product, we obtain saddlepoint formulas for inclusion probabilities in k-DPPs. These turn out to be extremely accurate, and suffer less from numerical difficulties than exact methods do. Our results also suggest that k-DPPs and DPPs also have equivalent maximum likelihood estimators. Finally, we obtain results on asymptotic approximations of elementary symmetric polynomials which may be of independent interest. Details may be found here and the code here.
Determinantal Point Processes for Graph Sampling
efficiently sampling bandlimited signals using repulsive point processes such as Determinantal Point Processes.
In an effort to improve the existing sampling theorems for graph signals, in terms of number of necessary nodes to sample, robustness to noise of the recovery, and/or complexity of the sampling algorithms; we propose to take a close look at determinantal processes. Building upon recent results linking determinantal processes and random rooted spanning forests on graphs, we investigate how particular random walks on graphs may end up revealing optimal sampling sets. Preliminary results using loop-erased random walks may be found here.
A Fast Graph Fourier Transform
does the Graph Fourier Transform admit a O(NlogN) algorithm like the classical FFT?
The Fast Fourier Transform (FFT) is an algorithm of paramount importance in signal processing as it allows to apply the Fourier transform in O(NlogN)
instead of O(N^2) arithmetic operations. Today, in graph signal processing, there are two computational bottlenecks regarding the graph Fourier transform: first, one needs to diagonalize the Laplacian matrix (or adjacency matrix, depending on what model you prefer) which costs O(N^3) operations; then, given a signal, one needs to multiply the obtained eigenvector matrix with the signal costing another O(N^2) operations.
To circumvent such issues,
we propose a method to obtain approximate
graph Fourier transforms that can be applied rapidly and stored
efficiently. It is based on a greedy approximate diagonalization
of the graph Laplacian matrix, carried out using a modified
version of the famous Jacobi eigenvalues algorithm.
[PDF] [The Faust Toolbox]
Compressive Spectral Clustering
combining graph signal processing
and compressed sensing to accelerate spectral clustering
We propose a compressive spectral clustering method that accelerates the
classical spectral clustering algorithm by bypassing the exact partial diagonalisation
of the Laplacian of the similarity graph and the k-means step at high dimension. It can
be summarised as follows:
1) generate a feature vector for each node by filtering
O(log(k)) random Gaussian signals on G;
2) sample O(k log(k)) nodes from the full set of nodes;
3) cluster the reduced set of nodes;
4) interpolate the cluster indicator vectors back to the
complete graph.
We prove that our method, with a gain in
computation time that can reach several orders of
magnitude, is in fact an approximation of spectral
clustering, for which we are able to control
the error.
Read more
Random sampling of bandlimited signals on graphs
How can one sample a k-bandlimited signal on a graph --i.e. a "smooth" signal whose
k first graph Fourier coefficients are non-null-- while still being able to recover
it perfectly?
The goals here are both to reduce as much as possible the number of samples, while
garanteeing robust reconstruction with respect to noise.
We propose a random sampling strategy that meets these goals while sampling only O(klog(k)) nodes.
Read more
Subgraph-based Filterbanks for Graph Signals
In order to design a critically-sampled compact-support
biorthogonal transform for graph signals, we propose
a design based on a partition of the graph in connected
subgraphs. Coarsening is achieved by defining one “supernode”
for each subgraph and the edges for this coarsened graph
derives from the connectivity between the subgraphs. Unlike the
“one every two nodes” downsampling on bipartite graphs, this
coarsening operation does not have an exact formulation in the
graph Fourier domain. Instead, we rely on the local Fourier
bases of each subgraph to define filtering operations. Using scalable algorithms to partiton nodes in well connected subgraphs (or communities), our proposition enables filterbank operations (compression, denoising...) in linear time.
[PDF] [Code]
Multiscale community mining in networks
Graph wavelets are recently developed tools that generalize the classical concept of wavelet analysis for signals defined on graphs. We take advantage of this precise notion of scale to develop multiscale community mining tools for networks.
Read more
Graph Empirical Mode Decomposition
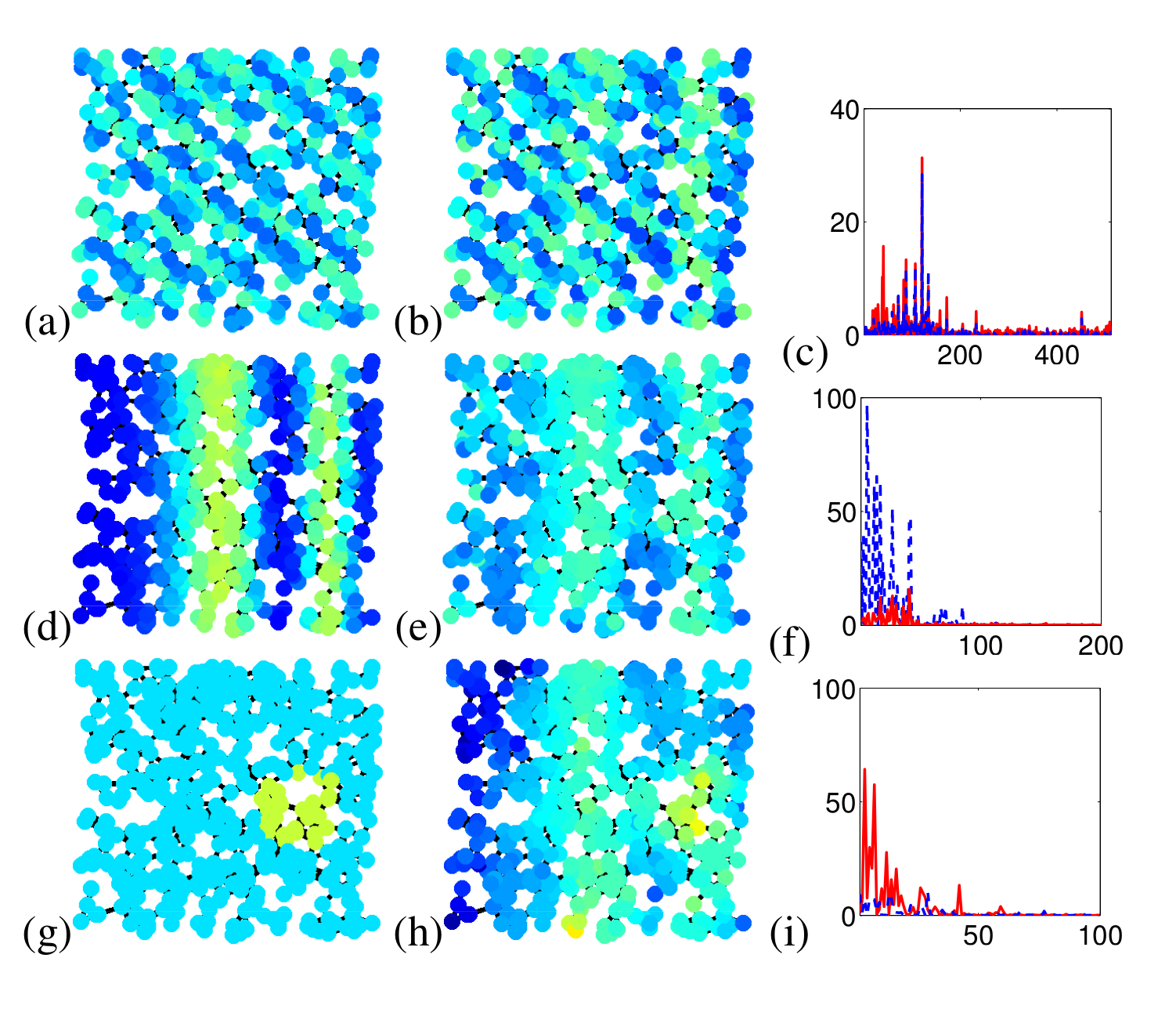Adaptation of the Empirical Mode Decomposition (EMD)
algorithm for signals defined on graphs.Read more
Bootstrapping in networks
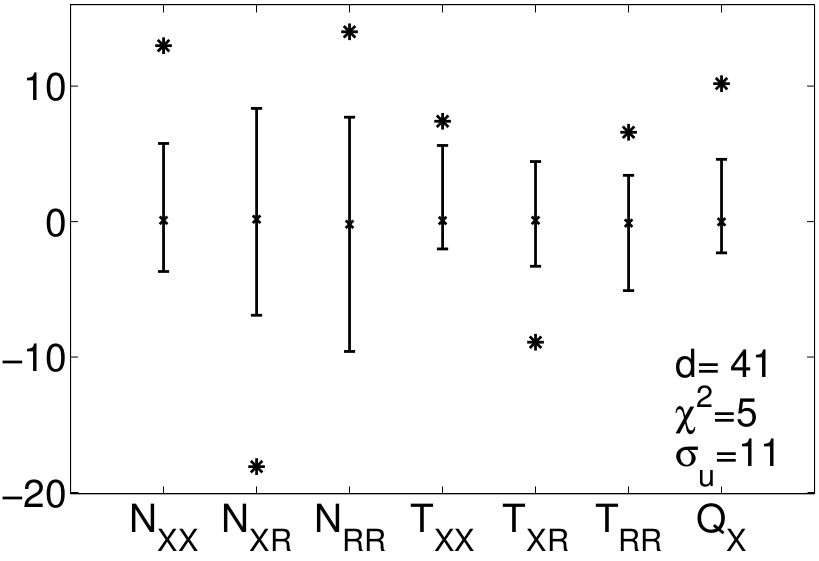In order to obtain statistics on measured observables in complex networks that are usually measured only once and hardly reproducible, one needs to adapt classical bootstrapping techniques to networks. Read more